Quasi-Experimentalism in Economics

Economics has always been an empirics-heavy discipline, with one foot in the ivory tower and another out in the real world. Adam Smith, the father of the field, may be most famous for The Wealth of Nations passages on the division of labor and on wealth disparities between countries, but less well remembered sections of the text delve into the weeds of observed trends in exchange rates, wages, and even grain prices. Smith did not benefit from the wonders of modern-day graph generators, but he cared enough about data to include tables with long lists of numbers instead. Fast-forwarding through the history of economics, one can observe that almost all the most celebrated of theorists—including Ricardo, Keynes, Hayek, and Solow, to name just a few—have put serious effort into reconciling their models with data.

What’s unique about empiricism in economics today is not, therefore, its empirical bent but a particular empirical paradigm that is becoming increasingly dominant in the literature: the experiment.

How, might you ask, does an economist run experiments? After all, we’re talking about the discipline that studies markets, prices, and the allocation of scarce resources—not exactly ripe territory for interventions in the name of science. But in fact, most economists working within this paradigm aren’t running experiments in a lab but are, rather, looking for processes that happen to occur naturally that happen to mimic the structure of experiments; these lucky accidents have come to be known as natural experiments or quasi-experiments in the economics literature.

How It Works

How do natural experiments work? It’s easiest to see through an example. A recent paper applying a quasi-experimental approach studied the famous elite public high schools of Boston and New York—the ones that require a high score on a special entrance exam to attend, like Stuyvesant, the Bronx High School of Science, and the Boston Latin School. Attendees of these schools tend to care more about school and get higher standardized test scores in grades K through 12 than their non-exam-school peers; they also get much higher SAT scores, are much more likely to attend college, and get accepted to much more selective institutions when they do. The question the researchers, Atila Abdulkadiroglu and his colleagues, wanted to answer is whether the experience of attending these elite high schools has anything to do with these students’ academic success. It’s possible that the environment at these schools, including, for example, being surrounded by peers who also got high entrance-exam scores and spend a lot of time studying, contributes to these students’ high SAT scores and acceptance at selective colleges. But it’s also possible that the students who get into elite high schools get the SAT scores they do because of traits they already possess by the time they enter high school, and would have been equally successful on the SATs and college applications even if they had attended a non-exam school instead. In the lingo of social science, this is a classic example of a question as to whether a particular outcome—in this case, high SAT scores—is the result of selection (of highly academically capable students into exam schools) or treatment (of actually attending those schools).

Abdulkadiroglu and his colleagues examine this question by exploiting a feature of the elite high school system. Admission is determined purely by performance on an entrance exam: if you get above a certain score you’re accepted; if you’re below, you’re not. Students who received scores just below the cutoff, then, are very similar to those who receive scores just above the cutoff, but those below end up going to non-elite high schools, whereas most of those who get accepted to an elite high school end up attending. By comparing the SAT scores of students just below and just above the cutoff, then, you can determine whether attending an elite high school causes students to get higher SAT scores: If the just-above-cutoff students do only a little better on the SATs then the just-below students, that can simply be explained by the fact that the just-above students were slightly better test takers to begin with; but if they end up doing a lot better, the only good explanation for the discrepancy is that the elite high school somehow turned them into better SAT test-takers than their just-below-cutoff non-elite-high-school peers. (This technique, exploiting a rule that assigns individuals, or firms, or whatever is being studied to one of two or more groups based on a numerical rule with a cutoff score, is known as using a regression discontinuity. )

But okay, “just above” versus “just below,” “a little” versus “a lot”—these terms are kind of vague and it sounds like there’s a lot of room for guesswork or, worse, manipulation to show the results the researcher wants to see, right? Well, economists have done a lot of work to determine how best to formally compare the “just below” and “just above” cutoff groups and how to figure out how big of a gap between their outcomes constitutes evidence of a treatment effect. Better yet, they have devised methods for transparently graphing the data in ways that provide visual evidence of a treatment effect, or lack thereof, that require little or no expertise in statistics to intuitively understand.

Take a look, for example, at the following graph:

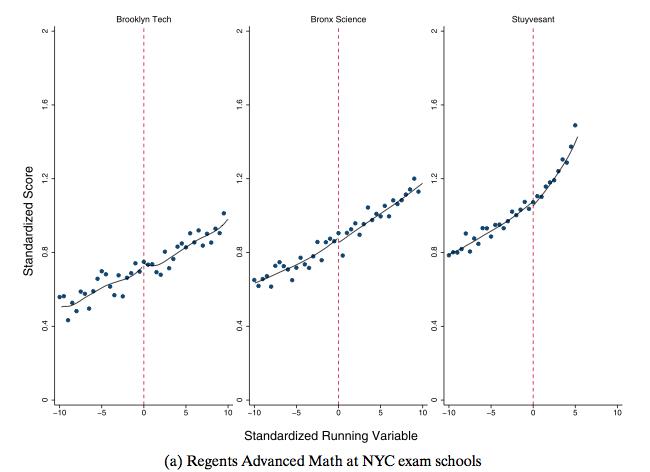
Source: Abdulkadiroglu et al, 2014

On the Y-axis is students’ scores on the New York Regents Advanced Math test, which is typically taken toward the end of high school and is a good indicator of SAT math performance. (“Standardized” just means that the scores are rescaled in a way that makes them easier to interpret and to compare with scores on other tests.) On the X-axis is scores on the entrance exam for New York City exam schools. There is one test for all three schools pictured, but each school has a different cutoff for entrance, and the scores in each panel are centered around the relevant school’s cutoff. So -5 in the Bronx Science panel indicates an entrance exam score 5 (standardized) points below the cutoff for entrance to Bronx Science, while +5 indicates a score 5 points above that same cutoff. To keep the graph from being overcrowded, not every student’s score is graphed individually; instead, each dot represents the average Regents score of students who got a particular score on the entrance exam. So, for example, the graph tells us that students who scored 5 points below the cutoff for Brooklyn Tech got an average standardized score of about 0.7 on the Regents.

The general upward trend of the plotted points indicates that, as you’d expect, students who got high scores on the high school entrance exam go on to get better scores on the Regents. Quick, before I reveal the answer, can you detect based on this graph whether attending an elite high school causes students to get higher Regents Math scores? If you think it does, try to imagine what a graph without a treatment effect might look like; if you think it doesn’t, try to imagine how a graph with a treatment effect might look.

The answer is that the graphs don’t show evidence of a treatment effect: The trend line rises at a fairly steady rate through the whole range of the graph; the cutoff for acceptance to an exam school has no discernible effect on that trend. If the exams school did cause higher Regents scores, the graph would look more like this graph (which is not real and strictly for the purposes of illustration):

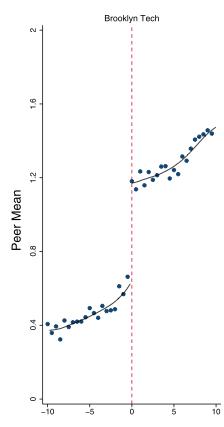
Source: Abdulkadiroglu et al, 2014

Despite going into high school with very similar scores, the students who made it into, for example, Brooklyn Tech, would have ended up noticeably ahead of students who didn’t make it in.

Very similar results (i.e. no treatment effect) hold for the Regents in English in New York and for similar exams in Boston, as well as, for Boston only, a measure of college attendance and a measure of college selectiveness (comparable data for New York was not available). So there you have it: evidence that attending an elite high school does not cause students to get better SAT scores or make them more likely to get accepted into selective colleges.

I hope you’ve also been convinced, along the way, that the technique of regression discontinuity can establish credible empirical facts. It’s far from the only quasi experimental technique; its most popular relatives in the quasi-experimental toolkit are called instrumental variables and difference-in-differences, which I won’t take the time to explain in as much detail but of which we will see some examples later in this piece.

A Very Brief History of Econometrics

Today, economists employ natural experiments to study everything from charter schools to democracy, labor market participation to fertility choices—an array of topics so vast that it can be hard to imagine how economists got by without these methods before they started gaining popularity, a mere 25 years ago.

As a matter of fact, the empirical realm of the field as a whole was much more fraught and subject to in-fighting and desperate soul-searching before quasi-experimental techniques were fully fleshed out. Up through the first half or so of the 20th century, theory reigned supreme throughout all subfields of economics. Typically, doing theory in economics involves creating a mathematical model to explain some economic puzzle or phenomenon, and supporting this model with a narrative of exactly what that model represents. Particularly within microeconomics, these models usually boil down to some sort of optimization problem subject to some constraints. A model might represent, for example, how a monopolist firm chooses its level of production by calculating the combination of output and price that maximizes its profit. As another example, drawn from labor economics, a model might sketch out a world in which individuals decide how to divide their hours between work and leisure based on the combination of income (determined by hours of work and wages) and leisure that they prefer most. Before you complain that this model is hopelessly detached from reality, since many hours of non-market work go uncompensated, note that economists have come up with versions of this model that also incorporate the decision to split time between market work and uncompensated housework, which they like to refer to as “home production.”

This state of affairs left the discipline, by the early-to-mid 20th century, flooded with theories but extremely short on empirical testing of those theories. A lack of substantiation for theory is a problem in itself, but it’s worth noting that it left economic theory vulnerable in two distinctive ways: First, economic decisions are very sensitive to the institutional conditions in which they are being made, which are all but impossible to theorize productively about without detailed empirical work. Second, for a complicated combination of historical and practical reasons, mainstream economic theory relies heavily on models of individual and firm behavior in which agents behave according to a very strict notion of rationality, and these models turn out to fail in systematic ways in the real world. That is, people and firms aren’t randomly irrational—which would be fine, in a way, since all models abstract to some degree from empirical noise—but that they do so predictably in particular directions in particular circumstances. It’s the systematic aspect of this issue that’s particularly damning, since it means that theorists could, in theory, come up with equally crisp, well-defined models that more accurately reflect human behavior and make better predictions.

The desire to bring theory into closer contact with empirical evidence dates at least as far back as the 18th century, when Sir William Petty and his intellectual allies sought to bring quantitative data to bear on economic policy questions in England, an approach that Petty called “political arithmetic.” Since then, efforts to engage in data-intensive projects in economics and on related policy questions has come in and out of fashion over the years. On the eve of the birth of modern efforts to study economics with data, this approach was decisively not in fashion: In 1912, the economist Irving Fisher, then vice-president of the American Association for the Advancement of Science, attempted to start a society to promote such efforts, but it drew so little interest that he gave up.

It was not until 1928 or so that Fisher and a few like-minded colleagues attempted the formation of such a group anew. By this point, the desire for a more statistics-heavy branch of economics had become more widespread, and so the Econometric Society was born in 1930. Meanwhile, Alfred Cowles, president of an investment counseling firm, became interested in commissioning empirical finance research, initially because he thought it might aid his firm’s investment advice. Following the 1929 stock market crash, however, he became more interested in funding empirical research in economics both for its own sake and for public purposes. So, in 1932, he established the Cowles Commission on Economic Research in Colorado Springs, with a mission of figuring out how to bring economic theory into contact with recently-developed statistical techniques. The Cowles Commission provided a crucial burst of funding and institutional support to these efforts.

A highly capable group of economists, statisticians, and mathematicians gathered to get to work in Colorado, and the group quickly established itself as the major driving force in the newly established sub-discipline of econometrics. What were they trying to do, exactly? Models devised by economic theorists involve parameters; for example, a mathematical model of the labor market might involve a parameter indicating how a laborer adjusts his hours of work in response to a change in his wages. The parameter is, ultimately, a number—it might tell us, for instance, that for every one-dollar increase in his or her hourly wages a worker will work 1.5 hours less per week. But theorists couldn’t fill in the numbers themselves—it took data to do that. Thus, the primary task of the econometrician, the thinking went, would be to figure out how to estimate the numerical values of these parameters using data.

Initially, Cowles Commission researchers and their colleagues anticipated that their task would be relatively narrow, because they imagined that the core work of economics would remain in the hand of theorists. Though many obstacles stood in the way of operationalizing early attempts to unite theory and data, chief among them was confronting the fact that raw observations, by their nature, often make it nearly impossible to estimate parameters of interest. Consider, for example, the problem of estimating how much an extra year of schooling causes an individual to earn, once they finish school and enter the labor market. Your first instinct might be to collect data on a whole bunch of workers’ earnings, along with how many years they spent in school, and compute the average relationship between these two variables. You’d almost certainly find that, in general, those who spend more years in school go on to earn more. Say you found, for instance, that an extra year of school is associated with 10% higher earnings at age 25. That might seem to be the parameter you’re looking for—but is it? It’s very possible, even likely, that this correlation is driven, to some extent, by the fact that the ability to do well in and stay in school also contributes to one’s ability to earn higher wages, regardless of the value of the schooling itself.

Say, again for the purposes of illustration, that even if everyone went to school for the same number of years, those who, in the real world, would have chosen to graduate from college earn 3% more than those who drop out in their junior or senior year. Then you might estimate that, for this group, the causal effect of schooling on earnings is only about 7%, or 10% minus the extra earnings the college graduates would have gotten anyway. But because, in the real world, we only observe one years-of-schooling choice and one salary at age 25 for each person, no number of observations will allow you to account for the bias associated with looking at a simple correlation between schooling and earnings.

The general issue of parameter estimation being confounded by unobservable or unmeasurable aspects of reality is such a pervasive problem in empirical work that it was given a name—the identification problem—and escaping it became a major goal of econometric research beginning in the 1940s and 50s. It might sound strange that econometricians spent such a long time working intently on what, in its simplest expression, is a pretty easy-to-understand problem; after all, how many potential solutions could there possibly be? But the identification problem can quickly become more complex in the context of large macroeconomic models with many moving parts, which, at this point, were econometricians’ main focus. Imagine, for instance, a model that lays out relationships between firms’ production levels, household consumption levels, employment, wages, interest rates, and inflation, over multiple periods in time, where many of the variables in the model are complicated functions of each other. Here, the biases associated with looking at correlations from raw data are much more difficult to analyze, and the types of techniques one might apply to try to resolve these biases are correspondingly much less straightforward.

Researchers’ first instinct was to put an even heavier burden on theoreticians. If the models specified in enough detail, based on a priori principles, exactly how the processes in their models worked, the identification problem could be resolved. To continue with the schooling and earnings example, imagine you somehow knew that individuals choose how many years to stay in school based entirely on their family background (e.g. how much their parents care about sending them to school) and on how much extra earnings they would expect to receive from spending more time in school. Their earnings are, in turn, determined by how much schooling they earn as well as their money-earning “ability,” which might include how capable or eager they are to sit at a desk for many hours. Suppose, further, that family background does not factor into this notion of money-earning ability.

Under these assumptions, it can be informative to compare individuals with different family backgrounds. That’s because, according to the model, family background influences the amount they will eventually go on to earn but only insofar as family background influences how long they stay in school. The individuals whose parents went to college, say, are more likely to go to college themselves than those whose parents only graduated from high school, and the family’s influence on their children’s later earnings stops at that. Then otherwise-similar individuals whose parents went to college will go on to earn more, on average, than their peers whose parents did not but only because their parents made them more likely to complete college. Thus, comparing the earnings and schooling attainment of otherwise-similar students with different family backgrounds can allow us to learn about the relationship between schooling and earnings.

The general approach of laying out detailed assumptions about a model based on what is deemed theoretically true or reasonable is often referred to as structural econometrics, and it describes economists’ primary approach to addressing the identification problem throughout the 1960s and 70s. Econometric researchers figured out exactly which sets of assumptions would allow parameters to be identified—in other words, resolving the identification problem—and which would not. Theorists then rose to the occasion and came up with models that were detailed and specific enough to satisfy the identification conditions the econometricians had come up with.

If this approach and the schooling example above seem hard to swallow, consider, first, that there are many cases where certain so-called structural assumptions seem more reasonable. In a competitive market, such as the market for cheap pencils, for instance, an empirical researcher can often gain a lot of leverage by assuming that firms in the market are all trying to maximize their profits, and that they will shut down if they are losing money. Sometimes, these sorts of assumptions are all it takes to resolve an identification problem.

Consider, also, a couple of directions in which the fleshing out of structural econometrics led: Clearly laying out all of the assumptions necessary for identification brought economists to more fully recognize their models’ fallibility, which motivated the development of procedures to test models rather than simply estimate their parameters. In other words, rather than leaving theory virtually entirely up to the theorists and their a priori assumptions, with empirical data limited to doing the job of filling in models’ quantitative details, new efforts gave data the job of testing whether the basic “story” embedded in a model could be believed or not. But beyond these efforts, and more importantly, laying out the types of assumption required for structural econometrics to resolve identification problems worked to draw out the contradictions and absurdities to which this approach could sometimes lead.

The schooling example, in fact, is drawn from a real paper written in 1979, toward the height of structural econometrics’ popularity but as established problems with the approach were starting to accumulate. The authors of this paper, Willis and Rosen, clearly recognized that their assumptions were untenable, but, working with then-available methods, were virtually forced into making them, because econometricians’ work had informed them what was required to avoid identification problems. They wrote, for instance, that distinctions between background variables that influence schooling choices and earnings capabilities were “increasingly difficult, if not impossible to make.” They defended their assumptions not on the grounds of plausibility but rather that “it provides a test of the theory in its strongest form,” acknowledging even then that “Certainly if the theory is rejected in this form there is little hope for it.”

Over the next several years, frustrations with econometric practices got articulated more explicitly. In 1983, Robert Leamer published a paper in the American Economic Review, one of the field’s top journals, entitled “Let’s take the con out of econometrics,” highlighting the uncomfortably important role of researchers’ whims in specifying theoretical assumptions, the sensitivity of empirical estimates to these assumptions, the implausibility of adequately testing these assumptions. Leamer states bluntly what many empirical economists of the day felt but were too polite to admit: “Hardly anyone takes data analysis seriously. Or perhaps more accurately, hardly anyone takes anyone else’s data analysis seriously.” He concludes by calling for fresh approaches.

Then, in 1986, Robert LaLonde published another paper in the same journal vividly demonstrating the issues laid out by Leamer in a specific context: The Manpower Demonstration Research Corporation had run an experiment in which qualified participants were randomly selected to participate in a job training program. LaLonde looked, first, at how much the job training program boosted participants’ incomes following participation, using the evidence from the government experiment. True experiments are not subject to the identification problem because participants don’t have any control over whether they’re selected to participate in the training program or not, so the group of participants is overall comparable to the group of non-participants. LaLonde then simulated what various contemporary econometric estimation techniques would have estimated the effect of the training program to be in the absence of experimental evidence, and found large discrepancies between the non-experimental techniques and the experimental one.

Many economists found Leamer’s arguments and LaLonde’s case study compelling and thus intensified their efforts to come up with alternatives to econometric practices then in use, and these efforts began to bear fruit beginning around 1990. In 1991, Angrist and Krueger published a paper taking a radically new approach to the problem of estimating the effect of schooling on earnings. It was not the first to study a natural experiment but one of the first to make a lasting impression on other researchers and contribute to the beginning of a movement. Rather than trying to solve the identification problem with some new approach to modeling or a new way of analyzing the usual data, they exploited a bureaucratic quirk that happened to mimic a lab experiment. They noticed, specifically, that U.S. states have laws concerning the age at which children must begin attending school, as well as the age teenagers must reach before they are legally permitted to leave high school, with the result that children born in different months may be legally required to attend school for different amounts of time. Depending on the time of year in which a child is born, say December, she might be required to start kindergarten relatively young, and would reach senior year of high school by age 17, the time she was legally permitted to drop out. But if she had instead been born in January, she might start kindergarten at a later age, and would only have reached junior year at age 17, and would be permitted to drop out then. It turns out that the students whose birth dates require them to at least begin senior year of high school are significantly more likely to graduate than those who are only, effectively, statutorily required to reach junior year. This fluke provides an opportunity to study the effect of high school graduation on later earnings: If children who are born at different times of the year are otherwise similar to each other, one can compare those required to reach junior year with those required to reach senior year to estimate the effect of graduating high school on earnings, and that’s exactly what the researchers did.

It’s worth taking a minute to appreciate just how much this approach differed from previous efforts to examine the relationship between schooling and earnings: First and foremost, the results were credible. If you accept the assumption that children born at different times of the year are comparable but for the legally mandated age at which they start kindergarten, all of the major statistical results of the study follow from there. This is in stark contrast to previous structural approaches which required numerous detailed assumptions to “solve” identification problems. Because the analysis is based upon exploiting a legal quirk rather than a parameter from a larger model, however, researchers learn something quite different from this sort of study than what they originally set out looking for: Whereas earlier researchers had imagined they might uncover a fairly general relationship between schooling and earnings, these authors can only say something about the relationship between high school graduation and earnings for students who have some risk of dropping out, which is much narrower and more specific.

The Angrist and Krueger paper was well received—most economists were happy to sacrifice generality for a big boost to credibility—but it remained to be seen whether its basic approach was just a one-off lucky break or something that could applied more broadly. Over the next decade or so, only a small number of additional papers in the quasi-experimental vein were published, few enough that most of them could be listed in a table, such as the one published in a paper focused by Angrist and Krueger, focusing specifically on instrumental variables, in 2001, from which this is an excerpt:

Source: Angrist and Krueger, 2001

Though small in number, these papers were very influential, and over the next decade the trickle of empirical work employing quasi-experimental techniques turn into a flood, which continues to this day.

The View from 2016

Zooming out, it’s tempting to describe the whole history of econometrics as a shift from model-based, theory-intensive approaches toward what the labor economist David Card calls a research-design-based approach, in which one of a relatively small set of empirical “templates” (instrumental variables, regression discontinuity, differences-in-differences, and some related variants of these) determine the basic formulation of studies. One problem with this summary is that in two major branches of economics, macroeconomics and the study of industrial organization, quasi-experiments represent only a tiny fraction of empirical work, primarily because opportunities for such studies are rare in these fields but also sometimes, particularly in the case of industrial organization, because structural assumptions are more tenable and so there is less need for quasi-experimental techniques. Econometricians working in these fields have done lots of work over the past several decades to reduce reliance on untenable assumptions, but because of the limitation of data in these subfields, it’s taken a different direction than that related to quasi-experiments. Second, even in the subfields of economics where quasi-experiments have become most prominent, including labor economics and public finance, economists still spend a lot of time running and analyzing regressions of non-experimental data, particularly in more exploratory work. Still, summarizing the history of empirical work in these disciplines as a shift from model-focused from research-designed-focused is not so far from the truth.

Looking back on the history, it’s tempting to ask why it took so long for economists to figure out that model-based econometrics could only, in most cases, lead to dead ends full of untenable assumptions and that achieving credibility would require more experimental style. Of course, it’s always easier to recognize flawed or wishful thinking in hindsight. It’s also easy to overlook the role of inertia in preserving a long-standing disciplinary norm of theory-centric work. This norm would have been much harder to question in the mid-20th century, as the types of datasets and computational resources necessary to employ quasi-experimental techniques at any appreciable scale did not yet exist. The invention and rise of modern computing has, of course, completely transformed that reality over the course of the past forty years, and therefore technology, too, has played a key role in the rethinking of econometrics.

Lastly, and most philosophically, an experimentally-inspired approach has required reconceiving, in many ways, exactly what economists are trying to do, and such deep shifts inevitably take time to sink in. When theory was king, economists often aspired to discover parameter values that nailed down core features of elegant models that described fundamental, unchanging features of the economy, much like a physicist might estimate the gravitational constant to be plugged in to Newton’s law or Einstein’s field equations—an analogy many economists were keen to make themselves. Quasi-experimental results are inherently much narrower and situation specific: Instead of attempting to figure out a general relationship between schooling and earnings, we have a very good estimate of the effect of graduating high school on earnings in 1980 by potential high school dropouts who were born in the U.S. in the 1930s, which might differ from those born in the 1940s, or in France, or among those who are not at risk of dropping out, and so on and so forth. And, so, the sacrifices in favor of credibility involved not just a humbling of ambitions but a more fundamental reconception of what the aims are.

The approach leaves hope for extrapolating from collections of credible empirical data points toward more general conclusions; and indeed, quasi-experimental methods have revealed plenty of patterns across different contexts. But the studies have also exposed enough variation across times and places and institutional settings that many economists have come to question what level of generality it ever made sense to aim for in the first place.

This kind of soul-searching is still ongoing—you can find it happening under the guise of conferences and journal symposia such as the one entitled “Con out of Economics” in the Journal of Economic Perspectives in Spring 2010—and is far from resolved. In the meantime, economists have continued to apply quasi-experimental techniques virtually anywhere they find the opportunity, no matter how far afield from the traditional bread-and-butter subjects of the discipline’s focus they might be. Graduate students hungry to get published will go searching for potential quasi-experiments related to any data set they can get their hands on. It’s hard to resist the impression that, for now, empirical work has gotten ahead of theory, and it’s far from clear whether theory will ever fully catch up.

But economists have given up neither on theory nor even on non-experimental empirical techniques. Quasi-experimental and experimental approaches have not come to monopolize what research gets done even in the subfields where they have become most popular, and few of even the most empirically focused of researchers completely neglect questions of how their results interact with theory. Researchers have also done work to help formalize the content of quasi-experimental empirical results within theoretical models. This work doesn’t do anything to make quasi-experimental evidence more general, but can help focus efforts to synthesize collections of results. Other work has made progress in uniting quasi-experimental approaches with more structural approaches to create hybrid beasts that many economists view as happy compromises between credibility and generality.

It can be hard to pick up on the existence of such efforts through the din of discussion related to economics in the media and in politics. The advent of quasi-experiments and, more broadly, the much greater availability of policy-relevant data, has greatly enhanced many policy debates but hasn’t come without concerning, or at least questionable, side effects. One issue is that an experimental study looked at in isolation is often a dangerous thing: An analysis showing charter schools increase students’ test scores in one city, for example, could lead to overconfidence in charter-promoting policies if there hasn’t yet been a study done showing that such schools are much less effective in another city with a different style of charter-school regulation.

Worse yet, as quasi-experimental studies proliferate, it becomes easier and easier for powerful people with already-established opinions to simply cherry pick studies that look to support their opinion. It’s rare that one study, or even several, could seal a case in favor of any controversial view—after all, these types of results are by their nature very context specific. But, judging by the content of many op-eds and speeches, the study-specific credibility of quasi-experimental evidence seems to often be just what’s needed to create the appearance of credibility in answering what is truly a much more complicated question. Meanwhile, even the studies that seem the most transparent and easy to understand often involve complicated enough statistics to leave room for statistical funny business, and the careful work that economists do to evaluate each others’ statistical procedures often gets ignored in these more public contexts. Less transparent work involving modeling and structural assumptions tends to never see the light of day outside seminar rooms, even in cases where the work is widely deemed credible by insiders in the discipline. Despite the diversity of work that gets done and discussed within the field, the demands of wider world can leave economists, effectively, playing the role of peddlers of isolated, context-dependent empirical facts to those eager to make use of them.

Perhaps I’m naïve, but I’m not so concerned about this state of affairs. I think that, taken as bodies of evidence, we have a lot to learn from quasi-experimental and experimental results. And I have some faith in the power of public debate to sort out which types of evidence to take seriously, and what they tell us and what they don’t, and to embed them in larger frameworks for thinking about the world—including ideological frameworks and moral ones—that are richer than more purely economic perspectives, and more up to answering the messy, fraught questions that political and social affairs so often bring up. As the primary purveyors of quasi-experimental evidence, economists will surely be a part of these discussions, and their theories will surely shape what they contribute to public debate. And if they have to contend with pundits, politicians, political scientists, or even (gasp) sociologists for attention in this debate, so much the better.

The Hypocrite Reader is free, but we publish some of the most fascinating writing on the internet. Our editors are volunteers and, until recently, so were our writers. During the 2020 coronavirus pandemic, we decided we needed to find a way to pay contributors for their work.

Leave a Tip

Help us pay writers (and our server bills) so we can keep this stuff coming. At that link, you can become a recurring backer on Patreon, where we offer thrilling rewards to our supporters. If you can't swing a monthly donation, you can also make a 1-time donation through our Ko-fi; even a few dollars helps!

The Hypocrite Reader operates without any kind of institutional support, and for the foreseeable future we plan to keep it that way. Your contributions are the only way we are able to keep doing what we do!

And if you'd like to read more of our useful, unexpected content, you can join our mailing list so that you'll hear from us when we publish.