Philip Engel
The Makings of a Mathematical Abstraction
ISSUE 9 | RECONSTRUCTION | OCT 2011

Coffered ceiling in the home of Baha-ud-Din Naqshband Bukhari, photo by Luis Bartolomé Marcos, licensed under Creative Commons Attribution-ShareAlike 4.0 International, via Wikimedia Commons
Suppose you were asked to define the number One. It feels very concrete; most would agree, “I know it when I see it.” So many things around us represent Oneness and reaffirm its validity as a concept: (a) the self, (b) Jerry Seinfeld, (c) God, (d) language, (e) Mom’s rocking chair, (f) this list, (g) et cetera, (h) a point, (i) nothing, (j) the universe, (k) France, (l) you, (m) things, and (n) the number of apples I ate today. Alas and alack, the solidity dissolves into nebulosity when we really try to put words to the concept. Our primary experience is not with the number, but its instantiations. In some sense, numbers cannot be constructed from more basic notions. They can only described—reconstructed from their characteristics.
Can’t you explain exactly what numbers are? What constitutes an explanation? Well, words; and what are words but elements of a language? But what language could we possibly use?
Mathematics! Care is required, though. Take the preceding paragraph: The single symbol “?” has four distinct senses—accusatory, questioning, rhetorical, and exasperated! Mathematical symbols, and their meaning, must be treated with great care and respect. Mathematics can provide the most certain kind of proof. A proof of what, you ask? Of the relations between numbers, the coincidences and the certainties. And not just the relations between individual numbers, but the relations between the relations! A proof is a thing of beauty, absolute and perfect. Like Mommy, it cannot, and will not, be argued with. The logic is so forceful, and so direct, that we are ineluctably drawn to the conclusion. It would be hypocrisy, dear reader, to claim that I always employ such logic, but I hope that you will feel its presence in the upcoming discourse.
How does one prove things? Mathematicians do so by manipulating numerical objects and their corresponding symbols creatively in a consistent, orderly way. The interplay of these two manipulations is often illuminating, and will help us on the long journey. If we’re going to prove statements using symbols, they must live in a delineated space and obey a delineated order. There is a pill you’ll have to swallow—ultimately it is one’s intuition which says that an idea has been faithfully transcribed into the language of mathematics. We can’t just work with an idea; we need to work with the translation of the idea, too. Furthermore, there is no turtle balancing mathematics on its back1—we’re beginning all alone, in the wildness of Chaos. Gulp.
Definition 1. The integers ℤ are what you get when you start with 1 and keep adding and subtracting it to stuff you’ve already got.
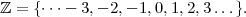
But wait—is this definition really adequate? For one thing, it refers to the concepts of “addition” and “subtraction” but doesn’t tell us what laws they obey. Come to think of it, it doesn’t tell us anything about the relations between numbers: addition, multiplication, subtraction, less than, et cetera. And really, these relations are important if we want to prove anything. How could we possibly present an argument of indubitable logic when we don’t even know what we’re assuming? Plus, our listing of the elements is meaningless—we still haven’t really said what they are or what properties they satisfy. It’s egregious! It’s almost as bad as successively putting apples on the table and saying, “See!?!?”
The inadequacies of Definition 1 far exceed inability to prove statements. We see that it is impossible to even make statements. What would it mean to “prove” something from Definition 1? The structure and the language just aren’t there. Clearly, we don’t have enough words yet to talk about ℤ.
Though the above definition sounds intuitive, it fails to answer any questions. For example, how do you know that you can’t get 7.3 by successively adding and subtracting 1? For that matter, in a world of integers, what is 7.3? Let’s try rephrasing: Find an x ∈ ℤ such that 10x = 73. (see The Appendix if you are unfamiliar with any symbols)
Let’s follow our own advice and avoid “constructions” of ℤ from now on. Instead, we’ll try to reconstruct it from its characteristics.
Suppose you were asked to describe ℤ. How would you do so? Facts like 2 ⋅ 3 = 6 or 1 + 1 = 2 don’t really cut it. We could write down an addition and multiplication table for all of ℤ, but that seems like an excessively large amount of information to describe what appears to be a relatively simple object.
We need to create a language which incorporates the structure of the integers inside of it. To do so, we’ll have to consider the structure of ℤ as a whole, instead of the properties of individual integers. As noted before, the integers have two operations—addition and multiplication. They are binary operations, viz., they have two inputs and one output. We could have even written +(a,b) instead a + b and ⋅(a,b) instead of ab, if we hadn’t been fucked in a while.
But there’s a storm cloud on the horizon. How do we convey (without hand-waving) that ab is multiplication and a + b is addition, as opposed to any old operations? It seems to be a task of similar difficulty to constructing One. For example, why isn’t it possible that addition and multiplication are switched?


So, multiplication and addition can only be defined with respect to each other, and themselves. Initially, this may seem off-putting. After all, aren’t addition and multiplication supposed to have real-life, geometric meaning? But that’s the joy of reconstruction—by requiring more and more properties of the integers, we will guide their path down one road of meaning, and this road not only reaches our geometric intuitions, but goes further. The properties gain a life of their own, leading us to new paths of mathematical discovery that were inaccessible before.
The moral is that addition and multiplication satisfy certain defining properties. E.g. the order of addition or multiplication is irrelevant to the answer: a + b = b + a and ab = ba. But properties of addition and multiplication aren’t sufficient to fully describe ℤ. For instance, there are special elements of ℤ, such as 0 and 1, and some numbers have minus signs.
To prove anything about the integers, we’ll have to write these
properties down, and hope they characterize ℤ. Furthermore, the
properties must derive from our intuition: They should be so simple
that we wouldn’t even dare question applying them in the real
world2.
If you wish, pause the article now, and write down basic properties of addition,
multiplication, negation, 0, and 1.
Leopold Kronecker, Philosophies of Mathematics:
God created the integers. All the rest is the work of Man.
Definition 2. The integers ℤ are a set with two operations + and ⋅ that satisfy the following properties:
- (Commutativity) a + b = b + a and ab = ba ∀a,b ∈ ℤ.
- (Associativity) (a+b)+c = a+(b+c) and a(bc) = (ab)c ∀a,b,c ∈ ℤ.
- (Distributivity) a(b+c) = ab+ac and (a+b)c = ac+bc ∀a,b,c ∈ ℤ.
- (Zero) ∃0 ∈ ℤ such that a + 0 = a and 0 + a = a ∀a ∈ ℤ.
- (One) ∃1 ∈ ℤ such that a1 = a and 1a = a ∀a ∈ ℤ.
- (Additive Inverses) ∃b ∈ ℤ such that a + b = 0 ∀a ∈ ℤ.
Definition 2 provides a delineated space of mathematical statements, and gives six assumed properties or relations, also called axioms. Even though they are quite basic, this set of properties has power. For example, we can now prove an important result about ℤ:
Proof. Consider two zero elements 0 and 0′. Then
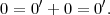
In a subtle way, this theorem was necessary to state property 6 because a + (-a) = 0 wasn’t well-defined until we knew that zero was unique, but let’s not go overboard with the rigor.
We don’t know yet that Definition 2 is a full definition of ℤ. What if there’s something missing? One way to test this is to see if we can derive other facts we intuitively know are true about ℤ. High from our previous proof and wild-eyed with newfound power, let’s bite off a more ambitious chunk of mathematical flesh. Suppose we try to prove that whenever ab = 0, either a = 0 or b = 0. Here’s the pickle: There are mathematical objects, different from ℤ, which satisfy properties 1-6, but in which this statement is false!
I present such a counterexample. The object (fake-ℤ) has six elements; we will denote them 0,1,2,3,4,5. To add, subtract, and multiply these elements, do so in the usual way, but then take the result, divide by 6, and return the remainder. For example, we have 3 + 4 = 1, and 2 + 4 = 0, and -2 = 4. Also, 2 ⋅ 5 = 4, and 5 ⋅ 3 = 3, and 1 ⋅ 0 = 0. We could in fact write down addition, multiplication, and inversion tables for fake-ℤ, as they would be finite in size, but the more abstract definition is easier to work with. The picture below is a visualization of this “clock arithmetic.” Adding goes counterclockwise and subtracting goes clockwise:

Fake-ℤ is feeling a bit dejected about being called as such, and has applied for a name change to ℤ6. But poor ℤ6 fails to satisfy the property that whenever ab = 0, either a = 0 or b = 0. This is because 2 ⋅ 3 = 0, but neither 2 nor 3 are zero. Of course, we could add a seventh axiom to our list which would banish ℤ6 from consideration, e.g. 2 ⋅ 3≠0, but one gets the distinct impression that this fact is neither fundamental to ℤ, nor will it solve the greater problem at hand.
Here’s the greater problem at hand: If a proof of the statement

The process of determining the axioms characterizing ℤ is one of reconstruction. Each time we write down a fact about ℤ we gain another silhouette of the integers. We glance at the light, then glance at the shadow cast, and acquire some knowledge of the true shape of ℤ. Each axiom casts a distinct shadow, and hopefully, from of all the shadows, we reconstruct ℤ.
Perhaps the “theorem” we were trying to prove was too fundamental, and must be taken as an axiom.
Definition 3. The integers ℤ are a set with two operations + and ⋅ that satisfy the following properties:
- Properties 1-6.
- If ab = 0, then a = 0 or b = 0.
Prove that Definition 3 fails:
Exercise 1. Construct ℤ5 as we constructed ℤ6. Are there nonzero a,b ∈ ℤ5 such that ab = 0? (No.) For which n does ℤn satisfy Property 2?
Having completed Exercise 1, we reach the same trouble we had before: ℤ
is very different from ℤ5 (for one, ℤ is infinite!) but our inventory is
not sufficiently fine to distinguish them. They both satisfy Definition 3.
What else is essential about ℤ? What naive thought have we not yet encapsulated? Sometimes the most difficult things to see are staring us in the face. What do the integers look like when we write them down? How do we categorize integers? These are somewhat leading, but difficult questions. If you wish, pause the article now, and try to write down a property organizing the humps and lumps of the integers.
A fundamental observation is that the integers are split up into three different components: The positives, the negatives, and zero. There is a distinguished subset of ℤ, called ℕ, of positive integers. This subset is special for a number of reasons. First, and most importantly, we feel like it is important. The positive integers (as opposed to negative integers) represent real things: profit (as opposed to debt) or creation (as opposed to destruction).
More concretely, the product or sum of any two positive integers is again a positive integer, and the operations of multiplication and addition have geometric interpretations on the positive integers, involving things like rectangles and lengths. But instead of attempting to explicitly describe ℕ, e.g. “ℕ is what you get when you add 1 to itself as many times as you want,
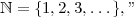
Somehow, the existence of ℕ captures the infinitude of the integers. The idea is that the ℤn’s are looping in circles, but ℕ precludes this possibility. After all, ℤn seems much more homogenous than ℤ. It’s hard (and in fact impossible) to say what would serve the role of ℕ for ℤn. It’s a frigging circle! With this in mind, I unveil the modern, tasteful, resplendent ℤ:
Definition 4. The integers ℤ are a set with two operations + and ⋅ that satisfy the following properties:
- Properties 1-6.
- There is a subset ℕ ⊂ ℤ such that
(Trichotomy) ∀a ∈ ℤ, exactly one of the following is true (EOOTFIT):
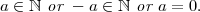
(Closure) ℕ is closed under addition and multiplication.
Closure (of a set) means that when you take two elements in the set and add or multiply them, the result is still in the set. Closure and trichotomy of ℕ ensure that ℤ5 is ruled out as a candidate for ℤ. Suppose ℤ5 has an ℕ, viz., there is a subset we’ll call ℕ5 of ℤ5 which satisfies trichotomy and closure. Then by trichotomy, there is element a ∈ ℕ5. Obviously if it’s closed, we can add a to itself as many times as we want without it leaving the set ℕ5. So a + a ∈ ℕ5, a + a + a ∈ ℕ5, etc. The point is that
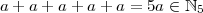
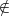 ℕ5.
ℕ5.
Not only was ℤ5 ruled out, but the whole class of examples ℤn was ruled out. We can play the same trick as before. If a ∈ ℕn, then by closure, we get a similar contradiction:
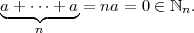
With more axioms comes more power. For example, we can now prove that which we so foolishly attempted to prove before:
Proof. Assume that neither a nor b is zero and we will derive a contradiction. By trichotomy, there are four cases:
- a ∈ ℕ and b ∈ ℕ
- a ∈ ℕ and -b ∈ ℕ
- -a ∈ ℕ and b ∈ ℕ
- -a ∈ ℕ and -b ∈ ℕ
Example case: Assume a ∈ ℕ and -b ∈ ℕ. By closure of ℕ under multiplication, a(-b) = -ab ∈ ℕ. Thus -ab≠0 by trichotomy. Hence ab≠0, a contradiction. The other three cases are similar. __
Thus, with Definition 4 we know we’re getting closer... the counterexamplegiver begins to sweat, pulling at his collar with a stubby, yellow finger. He attempts to loosen the necktie strangling around him, but just can’t seem to get a breath of air. Finally, the top button of his Oxford pops off, and he gasps,

The rational numbers ℚ satisfy all of the properties in Definition 4. You may ask, what serves as the subset ℕ? The answer is, of course, the positive rationals ℚ+. After all, every rational number is positive, negative, or zero, and the positive rationals are closed under addition and multiplication. But despite the failure, we’ve come a lot closer to describing ℤ.
Still, there’s clearly something wrong. Returning to the first equation posed, 10x = 73 is solvable in ℚ but not solvable in ℤ. So, there must be a property distinguishing them. Our intuition tells us that ℚ and ℤ are not the same object. The final observation, one that differentiates ℚ from ℤ, is that each integer is isolated from all others. This property is most difficult to formalize. In ℚ, a sequence of numbers can get closer and closer to a given value without actually reaching that value, for example

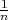 , then there is a smaller element
, then there is a smaller element 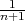 . Of course ℤ also has no least element, but
(and here is the key insight) ℕ does. The property that captures this is called
well-ordering.
. Of course ℤ also has no least element, but
(and here is the key insight) ℕ does. The property that captures this is called
well-ordering.
Well-Ordering. Every nonempty subset of ℕ has a least element.
But what does “less than” mean? The only reasonable way to define it given the tools available is that

The well-ordering principle gives pretty astounding results quite quickly. For example, we can prove an instance of what we called the “isolation” of numbers in ℤ—specifically, that there are no numbers between 0 and 1.
Proof. Consider the set
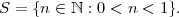
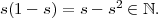
There is an alternative to the well-ordering principle, and that is the principle of mathematical induction. Induction formalizes our naive definition of ℕ: “start with 1, and keep adding it.”
Induction. If 1 ∈ S and S is closed under addition, then ℕ ⊂ S. In plain terms, suppose 1 is an element of an (infinite) set. If whenever n is in the set, n + 1 is also in the set, then that set contains ℕ.
It turns out that well-ordering and induction are equivalent! This makes some sense. They both seem to get at the isolation of the natural numbers, and they do so by invoking ℕ. Though induction seems a bit simpler in some ways, the well-ordering principle is easier to work with mathematically. No matter, we can deduce induction from well-ordering, then use it as much as we want: (Theorem 3 may be skipped if it is too difficult to follow.)
Proof. Suppose for the sake of contraction that induction is false. Then there is a set S such that 1 ∈ S and whenever n ∈ S we have n + 1 ∈ S, but ℕ is not a subset of S. Thus, the set
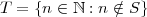
 T, since it is smaller than t, and t is the smallest
element of T. There can be only two reasons that t- 1
T, since it is smaller than t, and t is the smallest
element of T. There can be only two reasons that t- 1 T. Either t- 1 ∈ S
or t - 1
T. Either t- 1 ∈ S
or t - 1 ℕ.
ℕ.
Case 1: Suppose t - 1 ∈ S. then by the induction hypothesis,

 S. Contradiction.
S. Contradiction.
Case 2: Suppose t - 1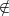 ℕ. Therefore t ≤ 1. Since t ∈ ℕ, and there are
no elements of ℕ between 0 and 1 by Lemma 1, we conclude t = 1. So 1
ℕ. Therefore t ≤ 1. Since t ∈ ℕ, and there are
no elements of ℕ between 0 and 1 by Lemma 1, we conclude t = 1. So 1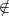 S.
But we assumed 1 ∈ S. Contradiction.
S.
But we assumed 1 ∈ S. Contradiction.
Thus, induction is proven. __
Aaah, isn’t this relieving? It does appear that our axioms have the power to prove anything! With induction proven, we easily conclude that ℕ is the smallest subset of ℤ containing 1 that is closed under addition, since all such subsets contain ℕ, and ℕ surely has this property. We’ve rigorized “keep adding 1.” Trichotomy tells us that every element of ℤ is either in ℕ, equal to 0, or has additive inverse in ℕ. So, the only elements of ℤ are: sums of 1 with itself, zero, and sums of -1 with itself. We’ve really locked onto what ℤ is!
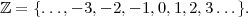
Definition 5. The integers ℤ are a set with two operations + and ⋅ that satisfy the following properties:
- Properties 1-6.
- There is a subset ℕ ⊂ ℤ such that
(Trichotomy) ∀a ∈ ℤ, EOOTFIT: a ∈ ℕ or -a ∈ ℕ or a = 0.
(Closure) ℕ is closed under addition and multiplication.
(Well-Ordering) Every nonempty subset of ℕ has a least element.
Or so we think.
There is not just power, but astounding power, in Definition 5. With it, we could prove some of the most difficult theorems in existence. But, shockingly, when we return to our original question, we fall short:
Proof. This proof will fail. Suppose for the sake on contradiction that there is such an x. We’d like to show 0 < x - 7 < 1, which contradicts Lemma 1. To show this, we’d like to show that 10 ∈ ℕ. Then we could get an equivalent inequality
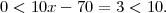
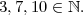
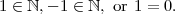
Perhaps you’ve seen the flaw. I used one of those accursed, slippery words in mathematics: “obviously.” If 1 = 0 then 1a = 0a, so a = 0 for all a ∈ ℤ. This flaw has directly given us the final counterexample:
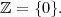
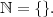
Hence, the addition of a single word to Definition 5 will correct our final, most trivial, problem:
Definition 6. The integers ℤ are a set with two operations + and ⋅ that satisfy the following properties:
- (Commutativity) a + b = b + a and ab = ba ∀a,b ∈ ℤ.
- (Associativity) (a+b)+c = a+(b+c) and a(bc) = (ab)c ∀a,b,c ∈ ℤ.
- (Distributivity) a(b+c) = ab+ac and (a+b)c = ac+bc ∀a,b,c ∈ ℤ.
- (Zero) ∃0 ∈ ℤ such that a + 0 = a and 0 + a = a ∀a ∈ ℤ.
- (One) ∃1 ∈ ℤ such that a1 = a and 1a = a ∀a ∈ ℤ.
- (Additive Inverses) ∃b ∈ ℤ such that a + b = 0 ∀a ∈ ℤ.
- (Naturals) There is a nonempty subset ℕ ⊂ ℤ such that
(Trichotomy) ∀a ∈ ℤ, EOOTFIT: a ∈ ℕ or -a ∈ ℕ or a = 0.
(Closure) ℕ is closed under addition and multiplication.
(Well-Ordering) Every nonempty subset of ℕ has a least element.
Now the kicker: Does ℤ exist?
Appendix
| Symbol | Meaning |
| ∈ | in |
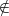 | not in |
| ⊂ | subset |
| ∀ | for all |
| ∃ | there exists |
 | implies |
| ⇐⇒ | if and only if |
| : | such that |
| {} | empty set |
1A well-known scientist (some say it was Bertrand Russell) once gave a public lecture on astronomy. He described how the earth orbits around the sun and how the sun, in turn, orbits around the center of a vast collection of stars called our galaxy. At the end of the lecture, a little old lady at the back of the room got up and said: “What you have told us is rubbish. The world is really a flat plate supported on the back of a giant tortoise.” The scientist gave a superior smile before replying, “What is the tortoise standing on?” “You’re very clever, young man, very clever,” said the old lady. “But it’s turtles all the way down!” — Stephen Hawking, A Brief History of Time
2Do you care if your apartment is 13x15 or 15x13?
3But wait a minute, stop everything! The train is coming to a halt at the Lebanon-Israel border and will now be inspected. The inspector has just confiscated all the papers. But what do all these symbols mean? We attempt to convey their meaning; nothing works. In fact we can’t even tell whether he speaks Hebrew or Arabic. All we know is that he’s started muttering to himself and pointing at the symbols. But what can he possibly get out of this—he’s trying to read it right-to-left! Luckily, a second man has come aboard and begins translating into English:
4“Reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons. It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.” — G. H. Hardy, A Mathematician’s Apology